Lösung :



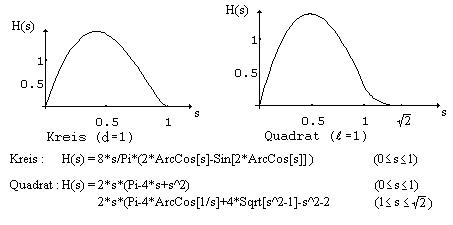
Aus der Verteilung der verschiedenen möglichen Abstände (Wahrscheinlichkeitsdichte) im Einheitskreis bzw. Quadrat folgen die beiden Mittelwerte für das Rätsel :
kreisförmiger Teich (d=7) :
mwk=7 * 64/(45*Pi) ~ 3.1689
quadratischer Teich (s=6) :
mwq=6 * (5*Log[Sqrt[2]+1]+2+Sqrt[2])/15 ~ 3.1284
Die Enten im quadratischen Teich sind sich also im Mittel näher !
©1998, by PiF

Beurteilung & Kommentar :

date: Thu Oct 22 11:13:12 1998
mweisgra@mail.zserv.tuwien.ac.at
Ecken überlappen unstetig - ich bevorzuge rundlicheres - andererseits hod des fiech zur Standardnormalverteilung eher keine positive Meinung
<-------------------------------------------------------------->

date: Thu Nov 26 19:25:29 1998
Thomas Krueger, krueger@hl.siemens.de

Mein Name sei Fun Jin. Ich lege also seine Kutte an und begebe mich ans Ufer des runden Teiches. Dort frage ich mich zunaechst, welchen durchschnittlichen Abstand E (wie Ente) das erste der beiden Entlein, dessen verschlungenen Weg ich nunmehr verfolge, denn von meinem Standpunkt I (wie Ich) haben mag.

Ah! Schon meine ich das Schulterklopfen des Meisters zu spueren, der mir wohl sagen moechte: "Gut, dass Du zunaechst ein Problem betrachtest, dass Deinem Gruenschnabelhirn auch angemessen ist!"

Nun frage ich also: "Wie gross ist die Wahrscheinlichkeit, dass meine Entfernung zum Entlein hoechstens x betraegt, dass sich die Ente also gerade auf dem Teil des Teiches befindet, der mir naeher ist als x?" Aber ja! Das ist f(x)/F, wobei F die Teichflae che und f(x) die Schnittflaeche des Teiches mit dem Kreis K vom Radius x und mit dem Mittelpunkt I ist.
Und die Wahrscheinlichkeit fuer einen Entfernungswert zwischen x und x+e ist somit (f(x+e)-f(x))/F, fuer sehr kleines e also e*l(x)/F, wenn l(x) die Bogenlaenge desjenigen Abschnittes des Kreises K ist, der auf dem Teiche verlaeuft.
Also werde ich x*l(x)/F 'ueber den Teich integrieren' muessen, um den gesuchten Wert E zu erhalten.

Ich verzichte daher auf die Berechnung von f(x) und widme mich gleich der Bogenlaenge:

l(x) = x * ( 2 * MIU ) = 2 * x * arccos(x/D)

Das erste Gleichheitszeichen gilt, wenn MIU der Winkel ist zwischen M=Teichmitte, I=Ich, U=Endpunkt des Bogens am Ufer. 2*MIU ist dann naemlich der Winkel unter dem mir der ganze Bogen erscheint und x*2*MIU ist also die Laenge des Bogens, der ja von mir die Entfernung x hat. Das zweite Gleichheitszeichen gilt wegen

cos(MIU) = (x/2)/R = x/D (R=Teichradius, D=Durchmesser).

Das Dreieck MIU ist naemlich gleichschenklig, die Hoehe von M auf IU landet also in der Mitte H, so dass x/2 die Ankathete im rechtwinkligen Dreieck MIH ist mit Hypothenuse MI der Laenge R.

Meine durchschnittliche Entenentfernung E liefert nun folgendes Integral:

E = integral (x=0,D) x*l(x)/F dx

F ist natuerlich (pi/4)*D*D. Also

E = ( integral (x=0,D) x*x*arccos(x/D) dx ) * (8/pi)/(D*D)

Ehrlich gesagt machen mich das Kauern am feuchten Teichufer und auch das elende Entengeschnatter nun doch ganz nervoes. Um mich besser auf die folgenden Rechnungen konzentrieren zu koennen, ziehe ich mich also in meine Studierkammer zurueck und widme mich hier ganz den Formeln und Zahlen. (Den wohlwollenden Blick des Alten habe ich zur Kenntnis genommen. Er weiss natuerlich, dass ich ohne meine Nachschlagewerke nicht mehr weiterkaeme.)

Aus der vorigen Gleichung folgt mit der Integraltafel (die sagt, das Integral ist (2/9)*D*D*D):

E(D) = 16/(9*pi) * D

Ich schreibe ab jetzt E(D) statt E, weil ich verschiedene Teichdurchmesser betrachten werde, um C(D), den durchschnittlichen Abstand zweier Entlein im runden Teich, zu berechnen.

Ich betrachte einen runden Teich mit Durchmesser 1+d, den ich mir in den inneren Teich (Durchmesser 1) und einen aeusseren Ring der Breite d/2 zerlegt denke. Fuer die Entenpositionen gibt es dann 4 Faelle, die zur folgenden Gleichung fuehren (die fuer genuegend kleines d fast richtig ist):

C(1+d) = p * p *C(1)
+ (1-p)* p *E(1)
+ p *(1-p)*E(1)
+ (1-p)*(1-p)*U(1)

Dabei sind p und 1-p die Wahrscheinlichkeiten, dass eine Ente im inneren Kreise bzw. im Uferring sitzt. E(1) ist eine gute Naeherung fuer den Abstand zwischen Innen-Ente und Ring-Ente. U(1) ist der (unbekannte) Abstand zweier Ring-Enten. p ist der Quotient der Flaechen des inneren und des gesamten Kreises. Also
p = 1/((1+d)*(1+d)) = 1/(1+2*d) = 1-2*d.

Achtung: Hier und im Folgenden bitte grosszuegig lesen "fuer sehr kleines d"!

C(1+d) = (1-4d)*C(1) + 2 * 2*d*E(1) + 0*U(1)

Da natuerlich C(x) = x*C(1) ist, folgt:

5*d*C(1) = 4*d*E(1)

Also unabhaengig von d und damit wieder exakt:

C(1) = (4/5) * E(1)

C(D) = (4/5) * E(D)

Also
C(D) = 64/(45*pi) * D

und endlich
C(7) = 448/(45*pi)
------------------

C(7) ist also knapp 10/pi und damit ungefaehr Pi. Oh! Jetzt also erkenne ich, dass es kein Zufall ist, wenn ein Ententeich eines Freundes der Zahl Pi einen Durchmesser von 7 Metern hat.

C(7) ist etwas groesser als Pi (naemlich 3,16895..). Na, dann wird S(6) vermutlich etwas kleiner sein als Pi. S(T) sei dabei die durchschnittliche Entfernung zweier Entlein auf einem quadratischen Teiche mit der Seitenlaenge T. Es geht also ohne Pause weiter (naschoen: ich habe zunaechst ein paar Tage geruht):

Schon hocke ich - diesmal nur in Gedanken - in einer der 4 Ecken eines quadratischen Teiches (Seitenlaenge 1). Ich betrachte die erste Ente und ignoriere alle Zeitraeume, in denen sie sich links der Diagonalen befindet. Ihre durchschnittliche Entfernung Q zu meiner Ecke wird dadurch nicht veraendert. Die Ente erscheint mir unter einem Winkel zwischen 0 und 45 Grad vom rechten Teichufer.Wenn dieser Winkel zwischen x und x+e liegt, ist die Entfernung zum gegenueberliegenden Ufer tan(x) (e sei wieder sehr klein!). Die durchschnittliche Entfernung zur Ente ist also (2/3)*tan(x), denn in einem Dreieck teilt der Schwerpunkt die Winkelhalbierende im Verhaeltnis 2:1. Der Flaecheninhalt des kleinen Dreiecks betraegt (e*tan(x))*tan(x)/2. Also:

Q = ( integral (x=0,pi/4) (2/3)*x*tan3(x)/2/F dx )

Dabei ist tan3 die dritte Potenz des Tangens. Diesmal ist F die halbe Teichflaeche, also 1/2.

Q = (2/3) * ( integral (x=0,pi/4) x*tan3(x) dx )

Die Integraltafel liefert moeglicherweise (neulich ging es, jetzt habe ich vergessen wie !!!....):

Q = (1/3) * ( wurzel(2) - ln ( wurzel(2)-1 ) )

Also ist Q(D) = D/3 * ( wurzel(2) - ln ( wurzel(2)-1 ) ).

Leider funktioniert der Trick mit dem schmalen Ringteich am Ufer diesmal nicht. Eine ganz neue Ueberlegung ist notwendig. ....

---- Wer fuellt diese Luecke !!!! ???? ----

Schliesslich: S(6) = 3,12..????

C(7) ist groesser als S(6). Im unserem quadratischen Teiche sind sich die Entlein also im Durchschnitt naeher als im grossen runden.

Ob der alte Moench zufrieden sein wird mit dieser Antwort?

Jetzt will ich noch etwas gestehen, das aber Meister Bun Li niemals erfahren darf: Heimlich habe ich mich in unsere klostereigene Rechenmaschine Virus (so heisst sie wirklich) hineingeschlichen und sie - rein gedanklich und ganz zufaellig versteht sich - 4 Milliarden Entenpaerchen auf die beiden Teiche flattern lassen. Unser kleiner Virus meditierte ein wenig und bestaetigte dann: S(6) ~= 3,128422 m, C(7) ~= 3,168955 m.

Zum Schluss ein Ausblick auf eine der noch anspruchsvolleren Fragen, die der Meister wohl auch bald stellen koennte: "Wie gross mag die Wahrscheinlichkeit dafuer sein, dass in einem bestimmten Augenblick das 'quadratische' Paerchen naeher beisammen ist als das 'runde'?" Wir haben ja hier noch nicht einmal bewiesen, dass sie groesser ist als 1/2 (Virus meint jedoch 0.51).

Leider war das erst die halbe Loesung. Aber da ich sehe, dass kaum jemand etwas einsendet, geht sie nun ab. Thomas

Bun Li sagt dazu :

Gut gerechnet, Grünschnabel,
leider hat es nicht bis zum Ende gereicht ! . . .Dieses eigentlich nicht lösbare Tan-Integral (ergibt eine unendliche Summe mit Bernoullizahlen) ist ja sehr merkwürdig !, und ergibt zudem einen anderen Wert als das darauffolgende (richtige) Q.

Der Mittelwert im Quadrat beträgt jedenfalls
(6/15)*(5*Log[Sqrt[2]+1]+2+Sqrt[2]) .

Zu Deiner Frage am Schluß : Die Wahrscheinlichkeit für einen bestimmten Augenblick beträgt ~ 0.508318 .
Es kann gezeigt werden, daß sie zumindest größer ist als

Dies folgt aus der allgemeinen Verteilung der Wahrscheinlichkeitsdichte.

Übrigens bedingt die größere Kreisfläche nicht immer auch einen größeren mittleren Abstand : Es existiert ein schmaler Bereich in dem sich die 'weitgestreckten Ecken' bei kleinerer Quadratfläche tatsächlich auswirken !


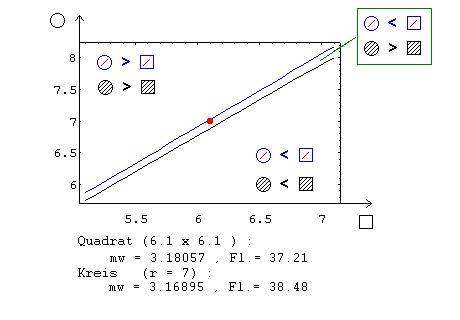
Bei der Wahl der Teich-Parameter hatte man also die Möglichkeit zwischen dem interessanten Bereich kleinerer Quadratfläche bei gleichzeitigem größeren Mittelwert; oder den schöneren ganzzahligen Werten, die ein Ergebnis ungefähr in der Nähe der Zahl Pi liefern.

<-------------------------------------------------------->
date: Tue Dec 8 16:29:23 1998
wilhelm@rz.uni-leipzig.de

Der betrachtete Vorgang findet in endlicher Zeit in endlich vielen gleichmäßig verteilten Schritten statt. Als arithmetisches Mittel aller möglichen Abstände ergibt sich dann die Hälfte des größtmöglichen Abstandes.
Die Diagonale des gegebenen Quadrates ist größer als der Durchmesser des gegebenen Kreises. Deshalb sind sich die zwei Entlein im kreisförmigen Teich im Mittel näher als die im quadratischen.
<----------------------------------------------------------->
date: Wed Dec 23 10:46:47 1998
Joachim Haberer, j.haberer@cogito.de

Zur Lösung des Rätsels kann ich nicht beitragen, aber der obige Zeitungsausschnitt ist in Japanisch geschrieben, nicht Chinesisch!(Chinesen haben keine Hiragana und Katakana, die man sofort erkennt ;-))
<---------------------------------------------------------------------->

date: Wed Jan 27 11:42:36 1999
Jens Willibald willibald@fzi.de

Unter der Annahme, dass die Enten punktfoermig sind und sich ueberall mit der gleichen Wahrscheinlichkeit aufhalten erhaelt man fuer den quadratischen Teich folgendes Integral
INT dx1 dy1 dx2 dy2 SQRT((x1-x2)^2+(y1-y2)^2) / Teichflaeche^2
die Normierung mit der Teichflaeche^2 ist noetig, da man zweimal ueber die gesamte Teichflaeche integriert hat. Die Teichflaeche ist natuerlich 36 m^2.
Fuer den Runden Teich ergibt sich (in Polarkoordinaten)
INT dr1 dr2 dphi1 dphi2 SQRT(r1^2+r2^2-2*r1*r2*cos(ph1i-phi2)) r1*r2 / Teichflaeche^2.
Die Teichflaeche betraegt hier PI*12.25 m^2.

Beide Integrale sind kaum analytisch zu loesen, daher habe ich mich fuer eine einfache Monte-Carlo-Integration mit zufaelligen Entenpositionen entschieden - je 20 Durchlaeufe mit 100000 Positionspaaren.
Diese ergab:

Quadratischer Teich:
Mittlerer Abstand = 3.1296 (min=3.1298, max=3.1396)
Runder Teich:
Mittlerer Abstand = 3.1483 (min=3.1418, max=3.1575)
Falls der Zufallsgenerator unter C vernuenftig war, bedeutet dies, dass der Mittlere Abstand im runden Teich groesser ist.

ciao Jens
<---------------------------------------------------------------------->

date: Mon Feb 22 14:50:32 1999
Werner Schaffenberger wes@bimgs5.kfunigraz.ac.at

Der mittlere Abstand zwischen zwei Punkten in einem Quadrat der Seitenlaenge a ist
d = (2 + sqrt(2) + 5 ln(1 + sqrt(2)) a / 15.
Fuer einen Kreis mit Radius r betraegt der mittlere Abstand
d=128 r / (45 Pi).
Setzt man r=3.5 und a=6 ein, so erhaelt man fuer den Kreis einen Abstand von d=3.169m und fuer das Quadrat einen Abstand von d=3.128m. Die beiden Enten sind einander also im quadratischen Teich im Mittel naeher.
Die Berechnung des mittleren Abstandes zwischen zwei Punkten einer Flaeche fuehrt auf ein vierfaches Integral. Die Berechnung dieses Integrals kann im Fall des Quadrats betraechtlich vereinfacht werden, wenn man die Symmetrien des Integranden ausnutzt. Im Fall des Kreises geht man auf Polarkoordinaten ueber und verschiebt das Zentrum zum Kreisrand.

Berechnung :

Der mittlere Abstand zweier Punkte einer beliebigen Fläche ist ein Vierfachintegral:

ist der Flächeninhalt der Fläche. Dieses Vierfachintegral muß nun für den Kreis und das Quadrat berechnet werden. Da der mittlere Abstand zweier Punkte offensichtlich proportional zur Seitenlänge des Quadrats beziehungsweise zum Radius des Kreises ist, genügt es, die Rechnung jeweils für ein Quadrat der Seitenlänge 1 und den Einheitskreis durchzuführen.

Quadrat

Der mittlere abstand zweier Punkte ist hier:

Versucht man jetzt direkt, die einzelnen Integrationen auszuführen, so ergeben sich sehr komplizierte Ausdrücke. Es ist daher sinnvoll, den Integranden erst noch umzuformen. Zunächst sieht man, daß das Integral unverändert bleibt, wenn man und vertauscht. Anstatt über das Einheitsquadrat in der -Ebene zu integrieren, genügt es, über das Dreieck zu integrieren. Das Integral über das Dreieck ergibt den selben Wert. Das Integral über das Einheitsquadrat in der -Ebene ist daher das Doppelte des Integrals über das Dreieck . Das Selbe gilt offensichtlich auch für und .

läßt sich daher schreiben als:

Statt und führen wir die Integrationsvariablen und ein:

Um diesen Ausdruck weiter umzuformen, betrachten wir folgendes Doppelintegral:

Wenn man dieses Integral bezüglich partiell integriert, so ergibt sich mit und :

Da und gilt, erhält man schließlich:

Statt eines Doppelintegrals steht auf der rechten Seite nun ein einfaches Integral. Wenden wir diese Formel auf unser Vierfachintegral jeweils für und an, so erhalten wir ein Doppelintegral:

Hier wurde statt und einfach und gesetzt. Wir haben somit das Vierfachintegral auf ein Doppelintegral zurückgeführt. Nun sieht man aber auch, daß dieses Integral bei Vertauschung von und unverändert bleibt. Daher gilt:

So, nun genug der Umformungen. Jetzt kommen wir zur Ausführung der Integrationen, die nun nicht mehr sehr aufwendig ist. Die Integration über gelingt mit der Substitution . Man erhält:

Setzt man die Integrationsgrenzen ein, so erhält man:

Die Integration über ist trivial:

Wenn man die Klammern auflöst, so erhält man entgültig für den mittleren Abstand zweier Punkte eines Quadrates der Seitenlänge 1:

Entsprechend gilt für ein Quadrat mit der Seitenlänge :

Kreis

Für den Einheitskreis gilt, wenn man zu Polarkoordinaten übergeht und den Kosinussatz anwendet:

Natürlich setzt man zunächst . Dann kann man eine der beiden Winkelintegrationen sofort ausführen und man erhält:

Nun kann man wieder die Symmetrie des Integranden bezüglich und ausnützen:

Und nun setzen wir :

Die Integration über läßt sich wieder leicht ausführen:

Jetzt muß nur noch das Doppelintegral über den Einheitskreis berechnet werden. Die Auswertung gelingt, indem man den Koordinatenursprung an den Rand des Kreises verschiebt (siehe Zeichnung).

Es gilt und . Jetzt müssen nur noch die Integrationsgrenzen für und ermittelt werden. Es gilt auch . Am Kreisrand ist . Daraus folgt . Für gilt daher:

Die Integration über ist ebenfalls leicht:

Daher ergiebt sich als mittlerer Abstand zweier Punkte im Einheitskreis:

Entsprechend ist der mittlere Abstand zweier Punkte in einem Kreis mit dem Radius :

<---------------------------------------------------------------------->

Der 1. Preis (Rätselbuch) wird für diese perfekte Lösung gerne vergeben !!
©1999, by PiF